“Say, What?”
That was my response the first time I read the “Sustained Inquiry” row in the PBLWorks Gold Standard PBL Project Design Rubric. I was completely at a loss about how to have students “pose questions, gather and interpret data, develop and evaluate solutions or build evidence for answers, and ask further questions” as the rubric described. I am a math teacher whose personal learning experience was to have the teacher do example problems on the board and then I do similar problems 15 to 40 times, depending on how many were in the textbook.
I later learned during a master’s class that this type of teaching is based on the behaviorist method. I also learned about constructivism, which is a method where students construct their knowledge with the support of a teacher. As I started to understand the definition of Sustained Inquiry, I discovered it is a mixture of these two primary methods of learning. For the last few years, I have worked to strike the right balance of these methods so that I can improve my implementation of projects. I knew great behaviorism strategies but I had no tools for constructivism. I learned about several methods and worked to implement them in my classroom. Here is what I have learned about how to use both methods in a project.
“Zooming” Problem Solving Process
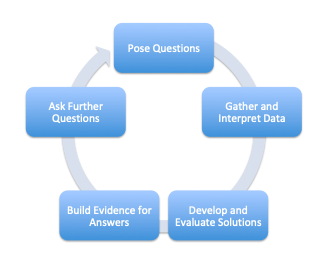
I have found the inquiry process to be somewhat circular, with posing questions and asking further questions to be the beginning and ending parts of a loop (see graphic below). It is often the most overlooked part when teachers are implementing projects. Many teachers have learned how to create a “Need to Know” list with students through PBLWorks PBL 101 workshops. Creating this list right after the entry event and driving question and referring to it every day is crucial. Many teachers struggle with keeping this list alive.
To help me do this, I have refined a tool that I call “Zooming”. Students begin to use it during the entry event and refer back to it each day until the project concludes. Here is how the tool is used:
- Students begin with zooming into the problem to write what they understand. They create a “what I know” list by viewing an entry document thats sets up the problem or need students will address in the project, the products to be completed, and some background information on the topic/objectives.
- Then they zoom out and formulate an initial idea of what the solution would look like, given what they know. For example, students may know they need to create a proposal, and may write what they know about writing a proposal.
- After they have an idea of a solution, they zoom out to create questions they need answered to create the product.
- They zoom in and out to write updated solutions based on their findings. The cycle repeats until students have a complete solution.
Seminar
As students’ questions drive the learning, you use tools to continue the process of gathering, interpreting, developing, evaluating and building information and products. One of my favorite strategies is a seminar (in particular the Paideia method), which is typically showcased in English. As the National Paideia Center states, a Paideia seminar is a collaborative intellectual dialogue facilitated with open-ended questions about a text (tangible items, such as a passage, painting, or a math problem). Students respond to a specific set of questions and also establish speaking and listening goals. I have used it as a tool to gather and interpret data as well as build evidence for answers. It deepens understanding of a concept during a project and develops communication and collaboration skills. For example, in my Finance Project, students complete a seminar on converting a savings formula into various forms, resulting in a different financial situation such as a loan. Some of the questions they tackle is how the formula A(t) =P( 1 + r⁄n )nt relates to B= A(1 + i )n + ((1 + p⁄i i )n - 1) and what does it mean mathematically to manipulate an equation.
Investigations
Sometimes a short lecture or modeling of a procedure is the best way to help students know a concept. Its efficiency is why many teachers use this behaviorist method so much. It has more power, though, when it is given to answer a question students have identified as one they need to know for the project. Before you deliver your lecture, share how it is answering one or more of the students’ questions. This is not the only way to teach students a math concept. Along my journey in trying to incorporate more constructivist strategies, I discovered investigations.
“Investigations” is a term I have given to activities or tasks that help students understand a concept and build knowledge to create a product. An investigation includes the following three traits: (1) uses questions or manipulation of an object to uncover a concept, (2) no requirement of didactic teaching by the teacher, and (3) includes appropriate support for students.
When done effectively, the investigation can complete all of the traits of sustained inquiry. In my book, Project Based Learning in the Math Classroom, which I co-authored with PBL Works National Faculty Member Chris Fancher, I provide an investigation for a geometry project. This investigation is based upon the students’ question, “What 3D shapes appear to be large but hold less volume?” The investigation is an adaption of Texas Instruments activity on 3D shapes. Here are some other math resources that are great for adapting to fit a project:
Continuing the Journey
Each year, I get better at balancing behaviorist and constructivist methods. There is no one right way but one essential ingredient. German mathematician, Georg Cantor, said it perfectly, “In mathematics the art of proposing a question must be held of higher value than solving it.” We have to move to valuing questions more than answers. It is the essential element in Sustained Inquiry that cannot be forgotten.

